Regresi Linier - Hitung Manual [1] - Slope Intercept
Kali ini kita akan coba melakukan regresi dengan hitung manual.
Bahan didapat dari Channel Youtube Statistic-101
NARASI KASUS
Di US sudah menjadi kebiasaan setiap pengunjung restoran memberikan tips buat pegawai restoran yang dikunjungi. Biasanya tips ini berhubungan dengan harga makanan yang di pesan. Makin mahal total harga makanan, makin besar tips yang diberikan pelanggan untuk waiter restoran tsb.
Misalkan kita adalah manager restoran. Kita dapat sample data sebanyak 6 observasi.
x y
BILL TIP
meal-1 5
meal-2 17
meal-3 11
meal-4 8
meal-5 14
meal-6 5
total 60
y rata2 10
Seharusnya variable x itu berisi harga dari meal-1, meal-2 sampai meal-6. Tapi anggap kita tidak tahu harganya. Sehingga dari 6 observasi itu hanya ada data 1 variable saja yaitu TIP.
Total TIP adalah $60, sehingga rata-rata per observasi $10 ($60/6 observasi).
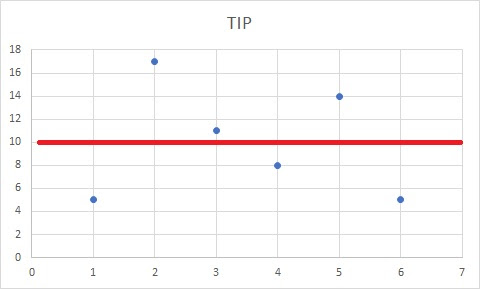
Sekarang kita gambar dalam scatterplot.
Nah, kita sudah punya satu model, untuk memprediksi berapa TIP yang akan diberikan jika ada meal baru, misal meal-7, dst bahwa TIP yang diberikan adalah $10.
Sekarang kita hitung berapa RESIDU atau ERROR dari 6 observasi tsb.
Sekarang kita kuadratkan (di-squrare-kan). Mengapa di kuadratkan?
1. Agar error negatif bisa jadi positif
2. Agar error yang > 1 akan berlipat-lipat sehingga mudah nanti memilahnya (karena nilainya membesar)
x y
BILL TIP Residu (error) error^2
meal-1 5 -5 25
meal-2 17 7 49
meal-3 11 1 1
meal-4 8 -2 4
meal-5 14 4 16
meal-6 5 -5 25
total 60 120 SSE = SST
y rata2 10
Terlihat diatas kita sudah dapat Sum of Square Error (SSE). Dalam hal ini karena variable hanya satu (yaitu dependent variable), maka SSE juga menjadi SST (Sum of Square Total).
SST 120 berarti Error maksimum yang bisa terjadi sebesar 120. Jika di cek pakai STATA sbb.
Tujuan dari pada Linear Regression adalah:
Meminimalkan nilai SSE Residual (atau memaksimalkan nilai SSE Model mendekati SS Total)
Sampai tahap ini dengan model garis lurus (y = 10, untuk x berapapun) kita dapat SSE nya 120 (dalam STATA disebut SS Total).
Sekarang, asumsi kita dapatkan harga dari meal (BILL) dan TIP yang diberikan spt berikut.
x y
BILL TIP
34 5
108 17
64 11
88 8
99 14
51 5
rata2 74 10 (Centroid 74,10)
Jika dilakukan scatter plot untuk 2 variable tsb, akan spt ini.
m = Gradient = Slope = b1
c = b0 = Intercept
Regresi linear upaya untuk adalah menemukan Slope dan Intercept yang tepat sedemikian sehingga SSE (dalam STATA SSE Residual jadi minimal).
Ingat pada model satu variable (hanya ada TIP), SSE telah dihitung menghasilkan nilai 120. Ini adalah SSE total atau maksimal.
Nah, sekarang jika pakai 2 variable, bagimana cara mencari Slope dan Intercerpt pada garis regresi?
Dengan rumus diatas kita hitung pakai Excel.
a b c=a/74 d=b/10 e=c*d f=c^2 g=e/f
BILL TIP
34 5 -40 -5 200 1600
108 17 34 7 238 1156
64 11 -10 1 -10 100
88 8 14 -2 -28 196
99 14 25 4 100 625
51 5 -23 -5 115 529
74 10 (rata2) 615 4206 0.146219686
didapat slope b1 = 0.146219686
y = b1x + b0
TIP = 0.14621986 BILL + b0
Maknanya: setiap kenaikan harga BILL $1 akan menaikkan TIP $15c ($0.1462).
Sekarang, bagaimana menghitung Intercept?
Rumusnya sbb:
b0 = y (rata2) - 0.14621986 x (rata2)
= 10 - 0.146219686 x 74
= -0.820256776
Jika di cek pakai STATA didapat hasil yang sama (kotak biru).
Persamaan garis regresi linear nya adalah y = mx +c
y = 0.146219686x - 0.820256776
Jika digambar pakai Excel, garis tsb (beserta formula yang dihitung Excel) tampak sbb.
Terlihat perhitungan Excel terhadap Slope cocok dengan perhitungan manual dan STATA.
Berapa SSE nya?
Terlihat SSE nya sekarang 30.07489301 (di STATA disebut SSE Residual)
Sehingga SS Residual (SSR) = SST - SSE
SSR = 120 - 30.07489301 = 89.92510699
Jika di cek dengan STATA, hasil perhitungan manual sesuai (kotak kuning).
Sekali lagi disampaikan bahwa Regresi Linier, adalah upaya agar SSR sekecil mungkin (atau SSM sebesar mungkin mendekati SST).
SSM = SST - SSR
KOEFISIEN KORELASI
Sekang kita bertanya: Seberapa besar Korelasi antara BILL dan TIP?
Rumus Pearson Corelation
r = b1 . (stdev x) / (stdev y)
b1 -- slope
Kita hitung pakai Excel. Rumus Standar deviation di Excel = STDEV (A1:A6), dan STDEV (B1:B6).
a b c=a/74 d=b/10 e=c*d f=c^2 g=e/f
BILL TIP
34 5 -40 -5 200 1600
108 17 34 7 238 1156
64 11 -10 1 -10 100
88 8 14 -2 -28 196
99 14 25 4 100 625
51 5 -23 -5 115 529
74 10 615 4206 0.146219686(slope)
29.00344807 4.898979486 (stdev)
Kita pakai rumus Pearson Correlation tsb:
r = 0.146219686 * 29.00344807 / 4.898979486 = 0.865665
r = 0.865665
Jika di cek pakai STATA, hasilnya sesuai.
. pwcorr tip bill
| tip bill
-------------+------------------
tip | 1.0000
bill | 0.8657 1.0000
Artinya kedua variabel berkorelasi positif cukup kuat sebesar 0.8657.
Lalu kita bertanya, apa makna MS (Mean Square error) untuk Model, Residual, dan Total? Dan apa makna Root Mean Square Error pada output STATA? Baca artikel lanjutan disini.









Comments
Post a Comment