Regresi Linear - Hitung Manual [2] - SS Residual Root MSE
Ini adalah artikel lanjutan dari sebelumnya. Jika Anda belum membacanya harap membaca artikel tsb terlebih dahulu.
MEAN SQUARE ERROR (MS Error)
Rumusnya adalah
MSE = SSE / N (N jumlah populasi)
MSE = SSE / df (df degree of freedom)
df = n - 2 (n jumlah sample observasi, 2 adalah 2 variable)
Karena kita menggunakan sample (sebanyak 6), bukan populasi, maka:
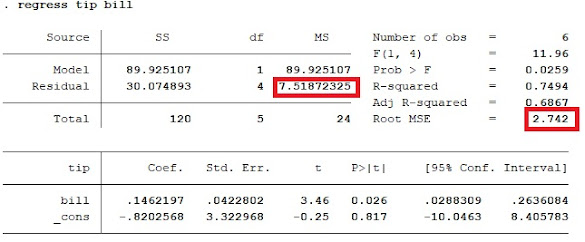
MSE = 30.07489301 / (6 - 2) = 7.518723252
Nilai ini sesuai dengan hasil STATA kotak warna merah.
ROOT MEAN SQUARE ERROR (s)
Root mean square error, atau kadang disebut standar error dari estimasi (ini mirip-mirip standar deviasi) adalah akar (root) dari MS Error.
Root MSE = sqrt (MSE residual)
Root MSE = sqrt ( 7.518723252 ) = 2.742029039
Root MSE dihitung manual didapat 2.742029039, sesuai dengan hasil STATA kotak warna merah.
Interpretasi:
Jarak rata-rata antara data-point TIP dengan garis regresi adalah senilai $2.742. Artinya jika anda sebagai manager restoran, ingin menetapkan berapa TIP yang pas untuk sebuah menu baru, seharga $20, maka ingat rumus garis regresinya:
y = 0.146 x 20 - 0.82 = $2.1
Jika RMSE diterapkan +/- $2.742, maka kisaran TIP maksimal yang masih wajar:
$4.842 sekitar $5.
Jika anak buah Anda kasih TIP $10 misalkan, maka ini bisa dibilang lebay.... :)
Nilai RMSE (atau standar error of the estimate) ini bisa memberikan gambaran seberapa bagus model dapat digunakan untuk bisa membuat prediksi. Apabila RMSE terlalu besar tentu berarti modelnya tidak baik untuk melakukan prediksi.
Selain itu RMSE dapat digunakan juga untuk membuat interval prediksi (dibahas lebih lanjut).
Kesimpulan untuk SSR MSR dan RMSE digambarkan sbb:
Perlu diingat bahwa:
SS Residual, MS Residual berada dalam nilai kuadrat. Sehingga nilainya jangan dibayangkan sebagai US$. Dimana SS Residual adalah nilai total seluruh observasi, sedangkan MS Residual apabila "dilihat" per observasi.
Akan tetapi Root MSE, atau estimasi standar error, ini sudah di lakukan operasi square (akar), sehingga bisa dibanyangkan dalam unit yang sama (yaitu US$).
R-squared (r^2)
Rumus dari R-squared adalah sbb:
R-squared = SSModel / SSTotal
= 89.92510699 / 120
= 0.749375892 ~ 75%
So far, kesimpulan Regresi Linear
Kita sudah liat dan dapat penjelasan tentang hal-hal yang penting dalam membaca output regresi liner di STATA. Antara lain:
1. SS Model mendekati SS Total
SS Model haruslah sebesar mungkin mendekati SS Total, dan SS Residual haruslah sekecil mungkin. Jika kondisi ini tidak tercapai maka model garis regresi kita tidak bagus.
2. R-squared yang besar
R-squared sebaiknya besar. Jika R-squred hanya kecil misal 20%, maka ini menyatakan bahwa variable independent mempengaruhi variable dependent sebanyak 20%. Artinya ada 80% variable lain yang tidak diketahui saat ini.
3. P > |t| nilainya kurang dari 5% (0.05)
Jika nilai ini > 0.05 maka hipotesis ditolak. Artinya model regresi liner tidak bagus, dan tidak bisa diterima.
4. 95% Conf. Interval tidak mengandung nilai 0
Artinya intervalnya harus >=0
5. Dapat juga ditambahkan Pearson correlation significant > 0.05, dan Kekuatan korelasinya diatas 0.3 atau diatas .5.
| Coefficient Value | Strength of Association |
| 0.1 < | r | < .3 | small correlation |
| 0.3 < | r | < .5 | medium/moderate correlation |
| | r | > .5 | large/strong correlation |
pwcorr Var1 Var2, sig star(.05) obs
EFEK DARI OUTLIER
Sebagai penutup, kita akan liat efek dari outlier.
Data awal adalah sbb:
. list bill tip
+------------+
| bill tip |
|------------|
1. | 34 5 |
2. | 108 17 |
3. | 64 11 |
4. | 88 8 |
5. | 99 14 |
|------------|
6. | 51 5 |
+------------+
Bagaimana kalau kita simulasikan baris ke 2, jika harga Bill 108, maka tip nya $1 (alih-alih $17). Apa yang akan terjadi?
Data kita ubah:
. replace tip = 1 in 2
(1 real change made)
. list bill tip
+------------+
| bill tip |
|------------|
1. | 34 5 |
2. | 108 1 |
3. | 64 11 |
4. | 88 8 |
5. | 99 14 |
|------------|
6. | 51 5 |
+------------+



Comments
Post a Comment